Selected Projects
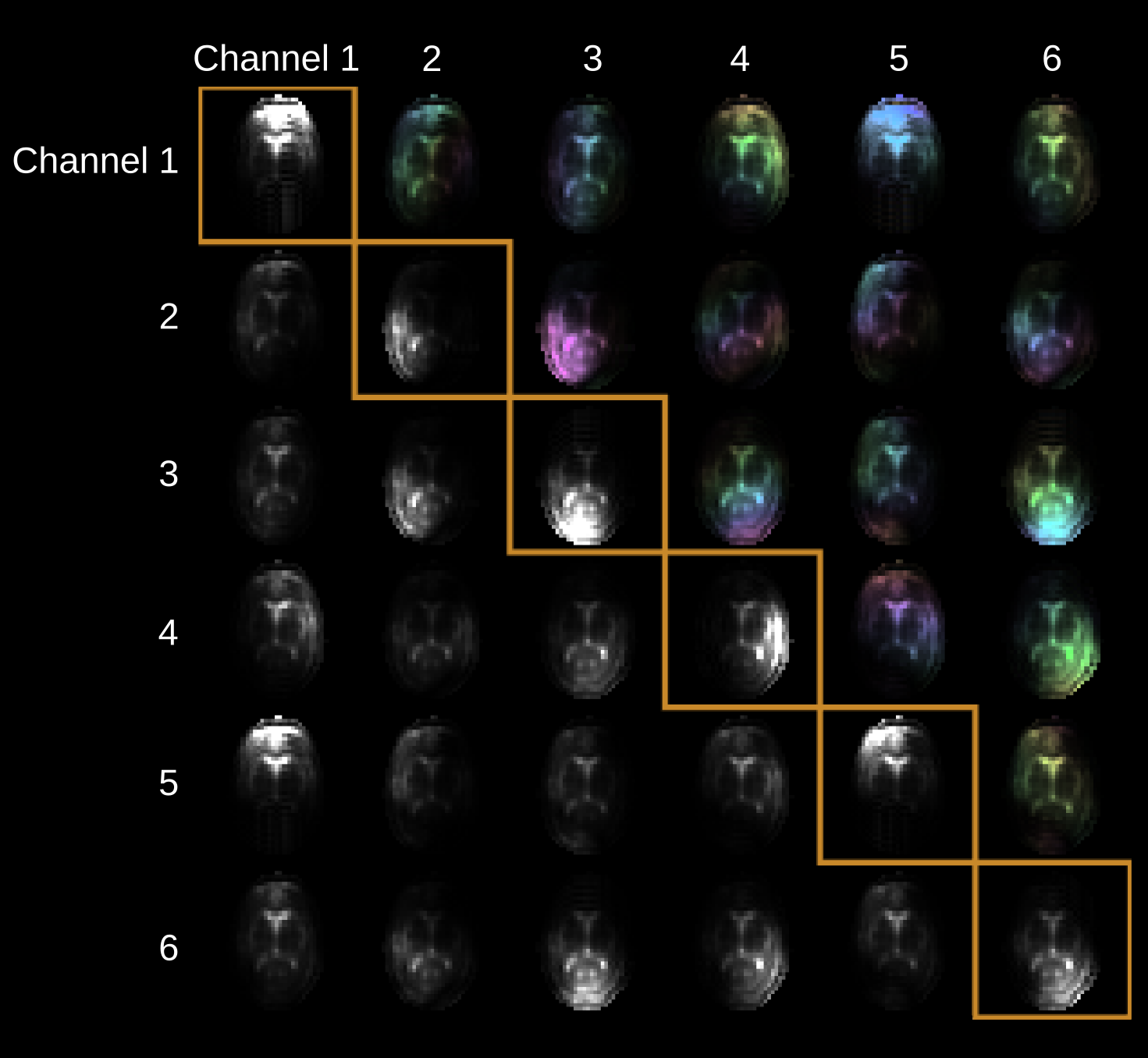
A Novel Hilbert-Space Reconstruction Framework for Computational Imaging
The modern image reconstruction landscape contains various approaches that achieve different compromises between image quality, speed, and transparency (e.g., deep learning methods are powerful but often black-box; classical methods are transparent but slow). In this project, I addressed the trilemma between quality, speed, and transparency by developing a novel framework for imposing image priors in reconstruction using reproducing kernel Hilbert space theory. This formulation enables fast and high-quality regularized reconstruction using single-pass convolutions rather than iterative solvers. It also provides transparency to the reconstruction methods by allowing one to directly inspect the image priors derived from the data.
References:
C.-C. Chan, J. P. Haldar, “Constrained MRI using weighted Hilbert spaces: Fast scan-specific reconstruction with transparent assumptions”, 2025. (Conference abstract under review). [Link]
Computationally Efficient Image Model for Non-Cartesian Fourier Imaging
In this project, I addressed a long-standing computational challenge (over 25 years) in non-Cartesian Fourier imaging (including magnetic resonance imaging (MRI), synthetic aperture radar, and radioastronomy) reconstruction by developing a computationally efficient image representation. A discrete representation of the underlying continuous image is a fundamental component of many methods for non-Cartesian Fourier-imaging reconstruction (whether classical or modern deep-learning methods). For over 25 years, the dominant approach has been the intuitive image-domain voxel-based representation, despite its well-known computational limitations. We conducted theoretical analyses and found that the challenge can be resolved by adopting a novel, theoretically-informed Fourier domain model. This new representation offers significant computational speedups while maintaining—and in some cases, surpassing—image quality compared to the conventional model.
References:
C.-C. Chan, J. P. Haldar, “A new k-space model for non-Cartesian Fourier imaging”, arXiv:2505.05647, 2025. (Under review). [Link]
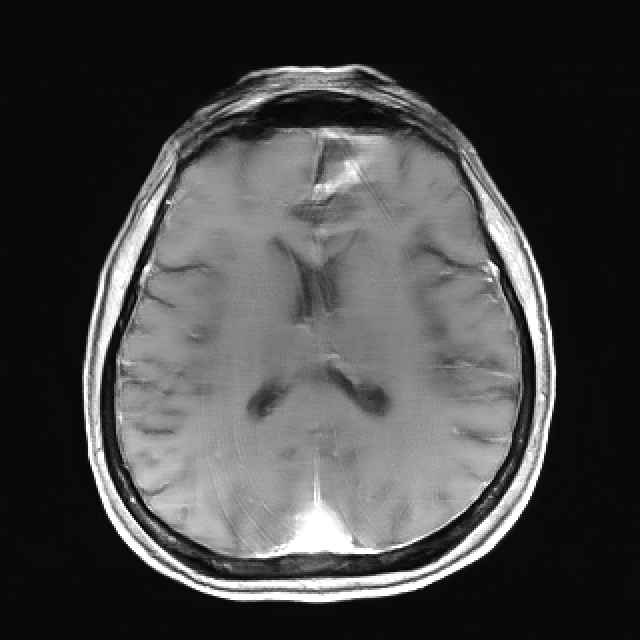
Resolution Analysis Framework for Modern Reconstruction Algorithms
Modern methods for image reconstruction are becoming increasingly nonlinear, black-box, and at risk of “hallucination”. These trends mean that traditional tools for judging confidence in an image (visual quality assessment, point-spread functions, etc.) are less helpful than before. In this project, I developed a computational framework that allows users to easily inspect how accurately important image features (e.g., abnormalities) are reconstructed by any reconstruction method.
References:
C.-C. Chan, J. P. Haldar, “Local perturbation responses and checkerboard test: A tool for characterizing advanced nonlinear algorithms for inverse problems in MR”, Magn. Reson. Med., vol. 86, pp. 1873–1887, 2021. [Link]
C.-C. Chan, J. Wang, T. Nadeem, J. P. Haldar, “On reference-based image quality assessment in medical image reconstruction: Potential pitfalls and possible solutions”, in Proc. Asilomar, 2023, pp. 36–39. (Invited paper). [Link]